Question

Find the area of a regular octagon with a perimeter of 80 ft and an apothem of 12.07 feet

Answer 1

The area of a regular octagon with a perimeter of 80 ft and an apothem of 12.07 feet is 482.8 ft².

Explanation:

An octagon is a polygon with eight sides. An octagon is regular (also called a regular octagon) is a polygon with all eight sides equal.

The apothem of a regular octagon is the shortest distance between the center and any of its sides, in other words, it is the distance that separates the center of the polygon from the central point of each side of the octagon.

The area is calculated using the following formula:

`Area=(n*L*Ap)/(2)`

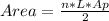
Where:

• n is the number of sides.
• L is the length of one of the sides.
• Ap is the value of the apothem.

Being n = 8 being an octagon and the perimeter P the sum of the sides of the octagon (P = 8 * L), the area of ​​the regular octagon can be calculated by:

`Area=(P*Ap)/(2)`

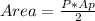
In this case:

• P=80 ft
• Ap=12.07 ft

Replacing:

`Area=(80ft*12.07ft)/(2)`

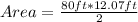
Solving:

Area=482.8 ft²

The area of a regular octagon with a perimeter of 80 ft and an apothem of 12.07 feet is 482.8 ft².