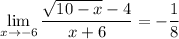*Silly and/or spam answers will not be tolerated* Evaluate the limit: \lim_(x \to -6) (√(10 - x)-4 )/(x + 6) Please explain how to rationalize and solve for the limit.

Question

*Silly and/or spam answers will not be tolerated*

Evaluate the limit:
`\lim_(x \to -6) (√(10 - x)-4 )/(x + 6)`
Please explain how to rationalize and solve for the limit.

Answer 1

`\displaystyle \lim_(x \to -6)(√(10-x)-4)/(x+6) =-(1)/(8)`

Explanation:

We want to evaluate the limit:

`\displaystyle \lim_(x \to -6)(√(10-x)-4)/(x+6) \\`

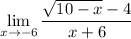
When attempting to evaluate a limit, we should always try direct substitution. This yields:

`\displaystyle \begin{aligned} &\Rightarrow (√(10-(-6))-4)/((-6)+6) \\ \\ &=(√(16)-4)/(-6+6)\\ \\ &=(4-4)/(-6+6)\\ \\ &=\underbrace{(0)/(0)}_{\text{Indeterminate}} \end{aligned}`

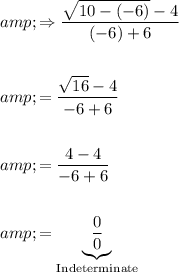
Since the result is an indeterminate form, we can try simplifying the limit.

Let's cancel the square root in the numerator. We can use the difference of two squares. Recall that:

`(a-b)(a+b)=a^2-b^2`

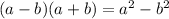
The expression in the numerator is:

`√(10-x)-4`

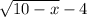
Therefore, to cancel it out, we will multiply it by:

`√(10-x)+4`

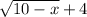
Multiply. This yields:

`=\displaystyle \lim_(x \to -6)(√(10-x)-4)/(x+6)\cdot(√(10-x)+4)/(√(10-x)+4) \\`

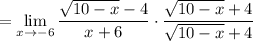
Simplify:

`\displaystyle \begin{aligned} &= \lim_(x \to -6)((√(10-x))^2-(4)^2)/((x+6)(√(10-x)+4))\\ \\ &=\lim_(x\to-6)((10-x)-(16))/((x+6)(√(10-x)+4))\\ \\ &=\lim_(x \to \ -6)(-x-6)/(x+6(√(10-x)+4))\end{aligned}`

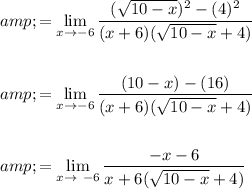
Factor:

`\displaystyle \lim_(x \to \ -6)(-(x+6))/((x+6)(√(10-x)+4))`

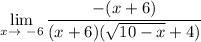
Cancel:

`\displaystyle \lim_(x \to \ -6)-(1)/(√(10-x)+4)`

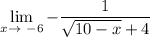
Now, we can attempt direct substitution again. Thus:

`\displaystyle \begin{aligned} &\Rightarrow -(1)/((√(10-(-6))+4))\\ \\ &=-(1)/(√(16+4))\\ \\ &=-(1)/((4+4)) \\ \\ &=-(1)/(8)\end{aligned}`

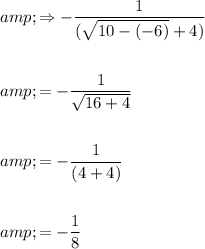
Therefore:

`\displaystyle \lim_(x \to -6)(√(10-x)-4)/(x+6) =-(1)/(8)`

Answer 2

-1/8

Explanation:

lim x approaches -6 (sqrt( 10-x) -4) / (x+6)

Rationalize

(sqrt( 10-x) -4) (sqrt( 10-x) +4)

------------------- * -------------------

(x+6) (sqrt( 10-x) +4)

We know ( a-b) (a+b) = a^2 -b^2

a= ( sqrt(10-x) b = 4

(10-x) -16

-------------------

(x+6) (sqrt( 10-x) +4)

-6-x

-------------------

(x+6) (sqrt( 10-x) +4)

Factor out -1 from the numerator

-1( x+6)

-------------------

(x+6) (sqrt( 10-x) +4)

Cancel x+6 from the numerator and denominator

-1

-------------------

(sqrt( 10-x) +4)

Now take the limit

lim x approaches -6 -1/ (sqrt( 10-x) +4)

-1/ (sqrt( 10- -6) +4)

-1/ (sqrt(16) +4)

-1 /( 4+4)

-1/8