Question

A test-preparation company advertises that its training program raises SAT scores by an average of at least 30 points. A random sample of test-takers who had completed the training showed a mean increase smaller than 30 points.

(a) Write the hypotheses for a left-tailed test of the mean.
(b) Explain the consequences of a Type I error in this context.

Answer 1

(a) Null Hypothesis,
`H_0` :
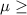`\mu \geq` 30 points

Alternate Hypothesis,
`H_A` :
`\mu` < 30 points

(b) Type I error is that we conclude that test-takers who had completed the training showed a mean increase smaller than 30 points but in actual, the program raises SAT scores by an average of at least 30 points.

Explanation:

We are given that a test-preparation company advertises that its training program raises SAT scores by an average of at least 30 points.

A random sample of test-takers who had completed the training showed a mean increase smaller than 30 points.

Let
`\mu` = average SAT score.

(a) So, Null Hypothesis,
`H_0` :
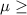`\mu \geq` 30 points

Alternate Hypothesis,
`H_A` :
`\mu` < 30 points

Here, the null hypothesis states that the training program raises SAT scores by an average of at least 30 points.

On the other hand, the alternate hypothesis states that test-takers who had completed the training showed a mean increase smaller than 30 points.

(b) Type I error states the probability of rejecting the null hypothesis given the fact that null hypothesis is true.

According to the question, the Type I error is that we conclude that test-takers who had completed the training showed a mean increase smaller than 30 points but in actual, the program raises SAT scores by an average of at least 30 points.

The consequence of a Type I error is that we conclude the test-takers have low SAT scores but in actual they have an SAT score of at least 30 points.