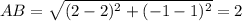Question

On a coordinate plane, a triangle has points (negative 5, 1), (2, 1), (2, negative 1).

Use the drop downs to answer the following questions about the distance between the points (−5, 1) and (2, −1).

What is the distance of the horizontal leg?

What is the distance of the vertical leg?

Use the Pythagorean theorem. What is the distance between the two points?

On a coordinate plane, a triangle has points (negative 5, 1), (2, 1), (2, negative 1).
Use the drop downs to answer the following questions about the distance between the points (−5, 1) and (2, −1).

What is the distance of the horizontal leg?

What is the distance of the vertical leg?

Use the Pythagorean theorem. What is the distance between the two points?

Answer 1

The answer are 7, 2 and 53

Explanation:

Answer 2

Explanation:

Given a triangle has points:

(-5,1),(2,1), (2,-1)

Let us label the points:

A(2,1),

B(-5,1) and

C(2,-1)

To find:

Distance between (−5, 1) and (2, −1) i.e. BC.

Horizontal leg AB and

Vertical leg, AC.

Solution:

Please refer to the attached diagram for the labeling of the points on xy coordinate plane.

We can simply use Distance formula here, to find the distance between two coordinates.

Distance formula :

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

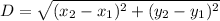
For BC:

`x_2 = 2\\x_1 = -5\\y_2 = -1\\y_1 = 1`

`BC = √((2--5)^2+(-1-1)^2) = √(63)`

Horizontal leg, AC:

`x_2 = -5\\x_1 = 2\\y_2 = 1\\y_1 = 1`

`AC = √((2-(-5))^2+(1-1)^2) = 7`

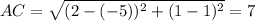
Vertical Leg, AB:

`x_2 = 2\\x_1 = 2\\y_2 = -1\\y_1 = 1`

`AB = √((2-2)^2+(-1-1)^2) = 2`