Question

What is the magnitude of the total acceleration of point A after 2 seconds? The bar starts from rest and has a constant angular acceleration of 1.0 rad/s2 clockwise.

Answer 1

a_total = 2 √ (α² + w⁴) , a_total = 2,236 m

Step-by-step explanation:

The total acceleration of a body, if we use the Pythagorean theorem is

a_total² = a_T²2 +
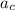`a_(c)`²

where

the centripetal acceleration is

a_{c} = v² / r = w r²

tangential acceleration

a_T = dv / dt

angular and linear acceleration are related

a_T = α r

we substitute in the first equation

a_total = √ [(α r)² + (w r² )²]

a_total = 2 √ (α² + w⁴)

Let's find the angular velocity for t = 2 s if we start from rest wo = 0

w = w₀ + α t

w = 0 + 1.0 2

w = 2.0rad / s

we substitute

a_total = r √(1² + 2²) = r √5

a_total = r 2,236

In order to finish the calculation we need the radius to point A, suppose that this point is at a distance of r = 1 m

a_total = 2,236 m