Answer:
Explanation:
Given function in the vertex form is,
f(x) = (3x + 13)² + 89
=
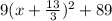 --------(1)
--------(1)
Vertex of the parabola →
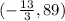
If the standard equation of this function is,
f(x) = 9x² + 2x + 1
We will convert it into the vertex form,
f(x) = 9x² + 2x + 1
=
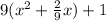
=
![9[x^(2)+2((1)/(9))x+((1)/(9))^(2)-((1)/(9))^2]+1](https://img.qammunity.org/2021/formulas/mathematics/high-school/7isumn67iracb4phd08hxf5lbmn2y4jor4.png)
=
![9[x^(2)+2((1)/(9))x+((1)/(9))^(2)]-9((1)/(9))^2+1](https://img.qammunity.org/2021/formulas/mathematics/high-school/gw70xiwl4fpd4tdyxlj8l9hmh5yxscwdq3.png)
=
![9[x^(2)+2((1)/(9))x+((1)/(9))^(2)]-((1)/(9))+1](https://img.qammunity.org/2021/formulas/mathematics/high-school/2zvauthnbm5c5mrg9d28hofz1bp9jwlbc5.png)
=
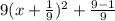
=
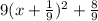 -------(2)
-------(2)
Vertex of the function →
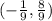
Equation (1) and (2) are different and both the equations have different vertex.
Therefore, given equation doesn't match the equation given in the vertex form of the function.