Question

Suppose babies born in a large hospital have a mean weight of 3316 grams, and a standard deviation of 324 grams. If 83 babies are sampled at random from the hospital, what is the probability that the mean weight of the sample babies would differ from the population mean by greater than 54 grams?

Answer 1

Answer: 0.129

Explanation:

Let
`\overline{X}` denotes a random variable that represents the mean weight of babies born.

Population mean :
`\mu= \text{3316 grams,}`

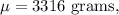
Standard deviation:
`\text{324 grams}`

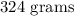
Sample size = 83

Now, the probability that the mean weight of the sample babies would differ from the population mean by greater than 54 grams will be :

`P(|\mu-\overline{X}|>54)=1-P((-54)/((324)/(√(83)))<\frac{\overline{X}-\mu}{(\sigma)/(√(n))}<(-54)/((324)/(√(83))))\\\\=1-[P(-1.518<Z<1.518)\ \ \ [Z=\frac{\overline{X}-\mu}{(\sigma)/(√(n))}]\\\\=1-[P(Z<1.518)-P(z<-1.518)]\\\\=1-[P(Z<1.518)-(1-P(z<1.518))]\\\\=1-[2P(Z<1.518)-1]=2-2P(Z<1.518)\\\\=2-2(0.9355)\ [\text{By z-table}]\\\\=0.129`

hence, the required probability = 0.129