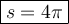Question

Arc length practice

Answer 1

`\large\boxed{s = 4\pi}`

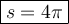
Explanation:

The arc length is determined by the formula
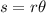`s=r\theta`, where s is the arc length, r is the radius, and
`\theta` is the value of the central angle (in radian formatting).

By substituting the values for the radius and the central angle, you can solve for the arc length.

`\text{The radius is half of the diameter -} \: \boxed{(4)/(2)=2}`.

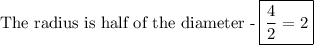The central angle is converted to radian form by multiplying the angle in degrees by the fraction of π/180 - 360° * π/180 = 360π/180 = 2π.

Now, substitute the values and solve for s.

s = (2)(2π)

`\large\boxed{s = 4\pi}`