Question

Given: D is the midpoint of AB; E is the midpoint of AC.

Prove: DE BC
y
Complete the missing parts of the paragraph proof.
Proof:
To prove that DE and BC are parallel, we need to show
that they have the same slope.
slope of DE = 12-11=_C-C
X2 - x1 a + b - b
A(2b, 2c)
D(b, c)
Ela + bc)
slope of BC =
B(0,0)
C(2a, 0)
Therefore, because
DE 1 BC.​

Answer 1

slope of DE = 0

slope Bc = 0

slopes are =

Explanation:

Answer 2

The lines DE and BC have the same slope, therefore the two lines, DE and BC, are parallel

Explanation:

To prove that DE is parallel to BC, we have;

The slope, m of the lines DE and BC are found from the following equation;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

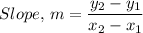
Where;

(x₁, y₁) and (x₂, y₂) = (b, c) and (a + b + c) for DE, we have;

`Slope, \, m =(c - c)/(a + b-b) = 0`

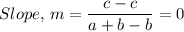
Where we have (x₁, y₁) and (x₂, y₂) = (0, 0) and (2a, 0) for BC, we have;

`Slope, \, m =(0 - 0)/(2a-0) = 0`

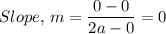
Therefore, because the lines DE and BC have the same slope, the two lines DE and BC are parallel.