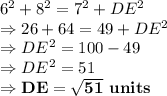Question

Point E lies within rectangle ABCD. If AE = 6, BE = 7, and CE = 8, what is the length of DE?

Answer 1

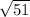`√(51)` units.

Explanation:

Point E is inside a rectangle ABCD.

Please refer to the attached image for the given statement and dimensions.

Given that:

Sides AE = 6 units

BE = 7 units and

CE = 8 units

To find:

DE = ?

Solution:

For a point E inside the rectangle the following property hold true:

`AE^2+CE^2=BE^2+DE^2`

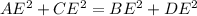
Putting the given values to find the value of DE:

`6^2+8^2=7^2+DE^2\\\Rightarrow 26+64=49+DE^2\\\Rightarrow DE^2=100-49\\\Rightarrow DE^2=51\\\Rightarrow \bold{DE = √(51)\ units}`