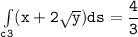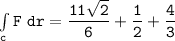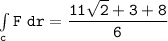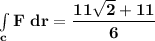Answer:
a.
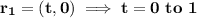
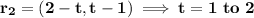
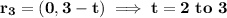
b.
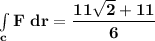
Explanation:
Given that:
C: counterclockwise around the triangle with vertices (0, 0), (1, 0), and (0, 1), starting at (0, 0)
a. Find a piecewise smooth parametrization of the path C.
r(t) = { 0
If C: counterclockwise around the triangle with vertices (0, 0), (1, 0), and (0, 1),
Then:
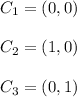
Also:
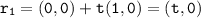
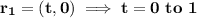
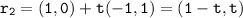
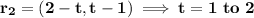
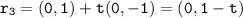
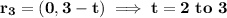
b Evaluate :
Integral of (x+2y^1/2)ds
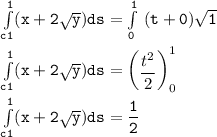
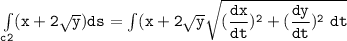
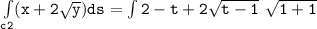
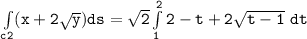
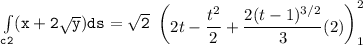
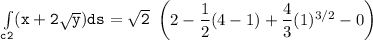
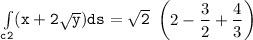
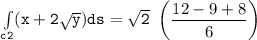
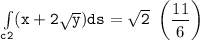
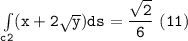
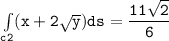
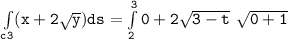
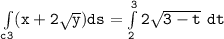
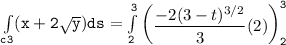
![\mathtt{\int \limits _(c3) (x+ 2 √(y)) ds = -(4)/(3) [(0)-(1)]}](https://img.qammunity.org/2021/formulas/mathematics/college/g95sio5l9iy2p4y87s7fewx7pn2du0io7v.png)
![\mathtt{\int \limits _(c3) (x+ 2 √(y)) ds = -(4)/(3) [-(1)]}](https://img.qammunity.org/2021/formulas/mathematics/college/lmyyt4du54sxboa3m2o6su9tyt4nr31rx0.png)