Answer:
the first partial sum
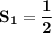
the second partial sum

the third partial sum
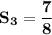
the fourth partial sum
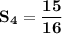
the fifth partial sum
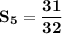
the sixth partial sum

Explanation:
The term of the sequence are given as :
 ,
,
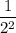 ,
,
 ,
,
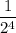 , . . .
, . . .
The nth term for this sequence is ,
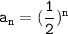
The nth partial sum of the sequence for
 is
is
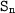
where;

The first partial sum is:
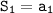

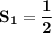
Therefore, the first partial sum
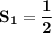
The second partial sum is:
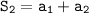
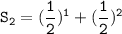

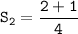

Therefore, the second partial sum

The third partial sum is :


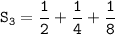
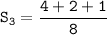
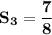
Therefore, the third partial sum
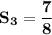
The fourth partial sum :
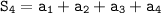
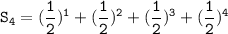
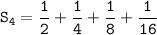
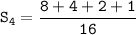
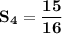
Therefore, the fourth partial sum
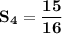
The fifth partial sum :

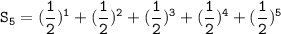
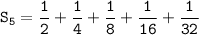
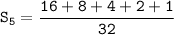
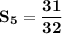
Therefore, the fifth partial sum
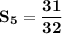
The sixth partial sum:

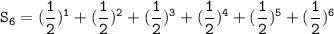
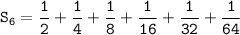


Therefore, the sixth partial sum
