Answer:
absolutely convergent
Explanation:
given data
sin(n)/3^n
solution
we have given term

when n = 1
and we know that
value of sin(n) ≤ 1
so that we can say that
 ≤
≤
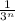 or
or
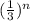
here
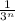 is converges this is because common ratio in geometric series
is converges this is because common ratio in geometric series
here r is
 and here it satisfy that -1 < r < 1
and here it satisfy that -1 < r < 1
so it is converges
and
 is also similar
is also similar
so it is converges
and here no
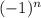 term is
term is
so we can say series is absolutely convergent