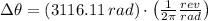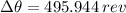Answer:
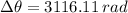 and
and
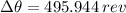
Step-by-step explanation:
The tub rotates at constant speed and the kinematic formula to describe the change in angular displacement (
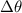 ), measured in radians, is:
), measured in radians, is:
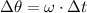
Where:
 - Steady angular speed, measured in radians per second.
- Steady angular speed, measured in radians per second.
 - Time, measured in seconds.
- Time, measured in seconds.
If
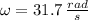 and
and
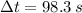 , then:
, then:
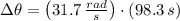
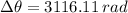
The change in angular displacement, measured in revolutions, is given by the following expression: