Question

A soda bottling company’s manufacturing process is calibrated so that 99% of bottles are filled to within specifications, while 1% is not within specification. Every hour, 12 random bottles are taken from the assembly line and tested. If 2 or more bottles in the sample are not within specification, the assembly line is shut down for recalibration. What is the probability that the assembly line will be shut down, given that it is actually calibrated correctly? Use Excel to find the probability. Round your answer to three decimal places.

Answer 1

The probability that the assembly line will be shut down is 0.00617.

Explanation:

We are given that a soda bottling company’s manufacturing process is calibrated so that 99% of bottles are filled to within specifications, while 1% is not within specification.

Every hour, 12 random bottles are taken from the assembly line and tested. If 2 or more bottles in the sample are not within specification, the assembly line is shut down for recalibration.

Let X = Number of bottles in the sample that are not within specification.

The above situation can be represented through binomial distribution;

`P(X=r)=\binom{n}{r} * p^(r)* (1-p)^(n-r);x=0,1,2,3,.....`

where, n = number of trials (samples) taken = 12 bottles

x = number of success = 2 or more bottles

p = probabilitiy of success which in our question is probability that

bottles are not within specification, i.e. p = 0.01

So, X ~ Binom (n = 12, p = 0.01)

Now, the probability that the assembly line will be shut down is given by = P(X
`\geq` 2)

P(X
`\geq` 2) = 1 - P(X = 0) - P(X = 1)

=
`1-\binom{12}{0} * 0.01^(0)* (1-0.01)^(12-0)-\binom{12}{1} * 0.01^(1)* (1-0.01)^(12-1)`

=
`1-(1 * 1* 0.99^(12))-(12 * 0.01^(1)* 0.99^(11))`

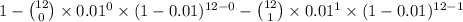
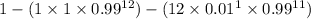
= 0.00617