Question

A researcher is interested in finding a 90% confidence interval for the mean number of times per

day that college students text. The study included 147 students who averaged 44.7 texts per

day. The standard deviation was 17.9 texts. Round answers to 3 decimal places where possible.

a. To compute the confidence interval use a tv distribution.

b. With 90% confidence the population mean number of texts per day is between

and

texts.

Answer 1

90% confidence the Population mean number of texts per day

(42.2561 ,47.1439)

Explanation:

Step(i):-

Given sample size 'n' = 147

mean of the sample size x⁻ = 44.7

standard deviation of the sample 'S' = 17.9

90% confidence the Population mean number of texts per day

`(x^(-) - t_(\alpha ) (S)/(√(n) ) ,(x^(-) + t_(\alpha ) (S)/(√(n) ))`

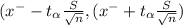
Step(ii):-

Degrees of freedom

ν=n-1=147-1=146

t₀.₁₀ = 1.6554

`(x^(-) - t_(\alpha ) (S)/(√(n) ) ,(x^(-) + t_(\alpha ) (S)/(√(n) ))`

`(44.7 - 1.6554 (17.9)/(√(147) ) ,(44.7 + 1.6554 (17.9)/(√(147) ))`

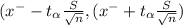
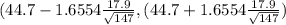
(44.7 - 2.4439 ,44.7 + 2.4439 )

(42.2561 ,47.1439)

Conclusion:-

90% confidence the Population mean number of texts per day

(42.2561 ,47.1439)