Answer:
The width (side perpedicular to the barn): x = 8 m
The lenght (side parallel to the barn): y = 16 m
Explanation:
x - the width of the barn
She has 32 m of fencing so for the lenght remain (32-2x) m of fencing:
y = 32 - 2x
Area of the fencing: A = x•y
A(x) = x•(32 - 2x)
A(x) = -2x² + 32x ← quadratic function
The maximum value of quadratic function occurs at:
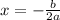
a = -2, b = 32

32-2x = 32 - 2•8 = 16