Question

A special tool manufacturer has 50 customer orders to fulfill. Each order requires one special part that is purchased from a supplier. However, typically there are 2% defective parts. The components can be assumed to be independent. If the manufacturer stocks 52 parts, what is the probability that all orders can be filled without reordering parts

Answer 1

0.65463

Explanation:

From the given question:

It is stated that 2% of the parts are defective (D) out of 50 parts

Therefore the probability of the defectives;

i.e p(defectives) =
`(N(D))/(N(S))`

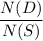
p(defectives) =
`(2)/(50)`

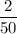
p(defectives) = 0.04

The probability of the failure is the P(Non-defectives)

p(Non-defectives) = 1 - P(defectives)

p(Non-defectives) = 1 - 0.04

p(Non-defectives) = 0.96

Also , Let Y be the number of non -defective out of the 52 stock parts.

and we need Y ≥ 50

P( Y ≥ 50) , n = 52 , p = 0.96

P( Y ≥ 50) = P(50 ≤ Y ≤ 52) = P(Y = 50, 51, 52)

= P(Y = 50) + P(Y =51) + P(Y=52) (disjoint events)

P(Y = 50) =
`(^(52)_(50)) ( 0.96)^(50)(1-0.96)^2`

`P(Y = 50) = 1326 (0.96)^(50)(0.04)^2`

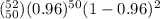
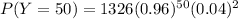
P(Y = 50) = 0.27557

P(Y = 51) =
`(^(52)_(51)) ( 0.96)^(51)(1-0.96)^1`

`P(Y = 51) = 52(0.96)^(51)(0.04)^1`

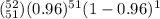
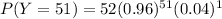
P(Y = 51) = 0.25936

(Y = 52) =
`(^(52)_(52)) ( 0.96)^(52)(1-0.96)^0`

`P(Y = 52) = 1*(0.96)^(52)(0.04)^0`

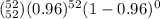
P(Y = 52) = 0.1197

∴

P(Y = 50) + P(Y =51) + P(Y=52) = 0.27557 + 0.25936 + 0.1197

P(Y = 50) + P(Y =51) + P(Y=52) = 0.65463