Question

One integer is
5 less than another. The sum of their squares is
157. Find the integers.

Answer 1

`\large \boxed{\sf \ \ 6 \ and \ 11 \ \ }`

Explanation:

Hello,

Let's note a and b the two numbers.

a = b - 5

`a^2+b^2=157`

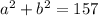
We replace a in the second equation and we solve it

`(b-5)^2+b^2=157 \\ \\ \text{*** develop the expression ***} \\ \\b^2-10b+25+b^2=157 \\ \\ \text{*** subtract 157 from both sides ***} \\ \\2b^2-10b+25-157=2b^2-10b-132=0 \\ \\ \text{*** divide by 2 both sides ***} \\ \\b^2-5b-66=0`

It means that the sum of the two roots is 5 and the product is -66.

because

`(x-\alpha )(x-\beta )=x^2-(\alpha +\beta )x+\alpha \beta \\ \\ \text{ where } \alpha \text{ and } \beta \text{ are the roots }`

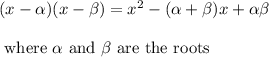
And we can notice that 66 = 6 * 11 and 11 - 6 = 5

So let's factorise it !

`b^2-5b-66=0 \\ \\b^2+6b-11b-66=0 \\ \\b(b+6)-11(b+6)=0 \\ \\(b-11)(b+6) =0 \\ \\ b=11 \ or \ b=-6`

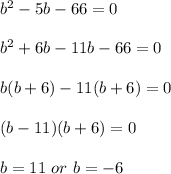
It means that the solutions are

(6,11) and (-6,-11)

I guess we are after positive numbers though.

Hope this helps.

Do not hesitate if you need further explanation.

Thank you