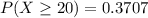Sixty percent of adults have looked at their credit score in the past six months. If you select 31 customers, what is the probability that at least 20 of them have looked at the…

Question

asked Oct 9, 2021 99.3k views

1 Answer

Gnawme · Answer 1 · 2021-10-14T12:35:20+0000

Answer:

The probability is
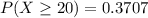
$P(X \ge 20 ) = 0.3707$

Explanation:

From the the question we are told that

The population proportion is p = 0.60

The sample size is n = 31

The mean is evaluated as

$\mu = n * p$

substituting values

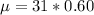
$\mu = 31 *0.60$

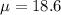
$\mu = 18.6$

The standard deviation is evaluated as

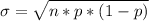
$\sigma = √(n * p * (1- p ))$

substituting values

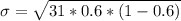
$\sigma = √(31 * 0.6 * (1- 0.6 ))$

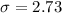
$\sigma = 2.73$

The the probability that at least 20 of them have looked at their score in the past six months is mathematically represented as

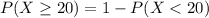
$P(X \ge 20) = 1- P(X < 20)$

applying normal approximation we have that

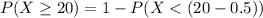
$P(X \ge 20) = 1- P(X < (20-0.5))$

Standardizing

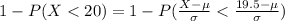
$1 - P(X < 20) = 1 - P((X - \mu )/(\sigma) < (19.5 - \mu )/(\sigma ) )$

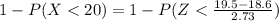
1 - P(X < 20) = 1 - P(Z < (19.5 - 18.6 )/(2.73 ) )

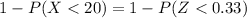
1 - P(X < 20) = 1 - P(Z < 0.33)

Form the standardized normal distribution table we have that

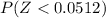P(Z < 0.0512) = 0.6293

=>
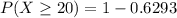
$P(X \ge 20 ) = 1- 0.6293$

=>
$P(X \ge 20 ) = 0.3707$