Question

Find the volume V of the solid obtained by rotating the region bounded by the given curves about the specified line. y = 5 36 − x2 , y = 0, x = 2, x = 4; about the x-axis

Answer 1

Answer: V = 193.25π

Explanation: The method to calculate volume of a solid of revolution is given by an integral of the form:

V =
`\pi\int\limits^a_b {[f(x)]^(2)} \, dx`

f(x) is the area is the function that rotated forms the solid.

For f(x)=y=
`(5)/(36)-x^(2)` and solid delimited by x = 2 and x = 4:

V =
`\pi\int\limits^4_2 {((5)/(36)-x^(2) )^(2)} \, dx`

V =
`\pi\int\limits^4_2 {((25)/(1296)-(10x^(2))/(36)+x^(4)) } \, dx`

V =
`\pi((25.4)/(1296)-(10.4^(3))/(108)+(4^(5))/(5)-(25.2)/(1296)+(10.2^(3))/(108)-(2^(5))/(5) )`

V =
`\pi((50)/(1296)-(560)/(1296)+(992)/(1296) )`

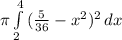
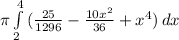
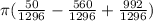
V = 193.25π

The volume of a solid formed by y =
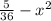`(5)/(36) - x^(2)` and delimited by x = 2 and x = 4

is 193.25π cubic units.