Question

consider the distribution of monthly social security (OASDI) payments. Assume a normal distribution with a standard deviation of $116. if one-fourth of payments are above $1214,87 what is the mean monthly payment?

Answer 1

`\mu = x - z(\sigma)`

`\mu = 1214.87 - 0.67(116) \\\\\mu = 1214.87 - 77.72 \\\\\mu = \$1137.15`

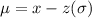
Therefore, the mean monthly payment is $1137.15.

Explanation:

What is Normal Distribution?

We are given a Normal Distribution, which is a continuous probability distribution and is symmetrical around the mean. The shape of this distribution is like a bell curve and most of the data is clustered around the mean. The area under this bell shaped curve represents the probability.

We are asked to find the mean monthly social security (OASDI) payment.

Mean monthly payment = μ = ?

We are given that the standard deviation is $116

One-fourth of payments are above $1214.87

One-fourth means 25%

`P(X > x )= P(Z > z ) = 0.25\\\\P(X < x )= P(Z < z) = 1 - 0.25\\\\P(X < x )= P(Z < z) = 0.75\\\\`

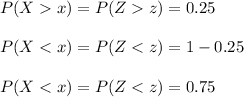
From the z-table, the z-score corresponding to 0.75 is found to be 0.67

`z = 0.67`

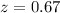
The mean is found by

`x = \mu + z(\sigma)`

`\mu = x - z(\sigma)`

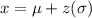
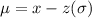
Where

x = $1214.87

z = 0.67

σ = $116

`\mu = 1214.87 - 0.67(116) \\\\\mu = 1214.87 - 77.72 \\\\\mu = \$1137.15`

Therefore, the mean monthly payment is $1137.15.