Question

Write an equation of the line passing through the given point and satisfying the given condition. Give the equation (a) in slope-intercept form and (b) in standard form.

(8,6); perpendicular to 2x - y = 4
(a) Write the equation of the line in slope-intercept form.

Answer 1

y = -
`(1)/(2)`x + 10

Explanation:

To find the equation of a line that passes through the point (8,6) and perpendicular to the equation 2x - y = 4, we will follow the steps below:

first write the equation 2x - y = 4 in a standard form

we will find the slope of our equation using this equation

2x - y = 4

y = 2x -4

comparing the above with

y = mx + c

m = 2

`m_(1)`
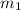
`m_(2)` = -1 ( slope of perpendicular equations)

2
`m_(2)` = -1

`m_(2)` = -1/2

our slope m = -1/2

We can now go ahead and form our equation

`x_(1)` =8
`y_(1)` =6

y-
`y_(1)` = m (x-
`x_(1)`)

y-6 = -
`(1)/(2)`(x-8)

y-6 = -
`(1)/(2)`x + 4

y= -
`(1)/(2)`x+4+6

y = -
`(1)/(2)`x + 10