Question

A system of linear equations includes the line that is created by the equation y = 0.5 x minus 1 and the line through the points (3, 1) and (–5, –7), shown below. On a coordinate plane, points are at (negative 5, negative 7) and (3, 1). What is the solution to the system of equations? (–6, –4) (0, –1) (0, –2) (2, 0)

Answer 1

Answer:The solution of the system of equations is (x,y) = (2,0)

Explanation:

Answer 2

The solution of the system of equations is (x,y) = (2,0)

Explanation:

The equation of a line through the points
`(x_1,y_1)` and
`(x_2,y_2)` is equal to:

`y-y_1=m(x-x_1)`

Where
`m=(y_2-y_1)/(x_2-x_1)`

So, the equation of the line through the points (3, 1) and (–5, –7) is:

`m=(-7-1)/(-5-3)=1`

`y-1=1(x-3)\\y=x-3+1\\y=x-2`

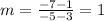
Then, we have two equations, y=x-2 and y=0.5x -1 , so solving for x, we get:

x - 2 = 0.5 x - 1

x - 0.5x = 2 - 1

x = 2

Replacing x=2 in the equation y=x-2, we get:

y =2 - 2 = 0

Finally, the solution of the system of equations is (x,y) = (2,0)