Answer:
The time interval required to lift the spacecraft to this specified height is 123.94 seconds
Step-by-step explanation:
Height through which the spacecraft is to be lifted = 32.0 m
Mass of the spacecraft = 260.0 kg
Four crew member each pull with a power of 135 W
18.0% of the mechanical energy is lost to friction.
work done in this situation is proportional to the mechanical energy used to move the spacecraft up
work done = (weight of spacecraft) x (the height through which it is lifted)
but the weight of spacecraft = mg
where m is the mass,
and g is acceleration due to gravity 9.81 m/s
weight of spacecraft = 260 x 9.81 = 2550.6 N
work done on the space craft = weight x height
==> work = 2550.6 x 32 = 81619.2 J
this is equal to the mechanical energy delivered to the system
18.0% of this mechanical energy delivered to the pulley is lost to friction.
this means that
0.18 x 81619.2 = 14691.456 J is lost to friction.
Total useful mechanical energy = 81619.2 J - 14691.456 J = 66927.74 J
Total power delivered by the crew to do this work = 135 x 4 = 540 W
But we know tat power is the rate at which work is done i.e
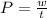
where p is the power
where w is the useful work done
t is the time taken to do this work
imputing values, we'll have
540 = 66927.74/t
t = 66927.74/540
time taken t = 123.94 seconds