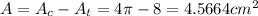Question

Find the area of the shaded regions.

Answer 1

`A = A_c-A_t=4\pi -8=4.5664cm^2`

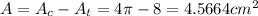
Explanation:

The area of the shaded region can be calculated as the area of the semicircle less the area of the right triangle.

The area of the right triangle can be calculated as:

`A_t=(b*h)/(2) =(LM*MN)/(2)`

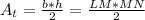
Where LM and MN have the same length because the internal angles are L=45°, M=90°, and N=45°. So the area is:

`A_t=(4*4)/(2)=8`

The diameter of the circle can be calculated using the Pythagorean theorem as:

`D=√((LM)^2+(MN)^2) =√(4^2+4^4)=4√(2)`

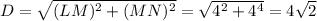
So, the radius is
`r=2√(2)`

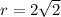
Finally, the area of the semicircle is:

`A_c=(\pi*r^2 )/(2)=(\pi*(2√(2))^2 )/(2)=4\pi`

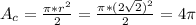
So, the area of the shaded region is:

`A = A_c-A_t=4\pi -8=4.5664cm^2`