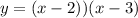Question

find the zeros or x-intercepts (values of r and s) of a quadratic relation y=x^2-5x+6 by factoring using the sum and product method

Answer 1

`y = x^2 -5x +6`

And for this case we want to find the zeros or x interceps r and s so we want to rewrite the function on this way:

`y = (x-r) (x-s)`

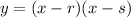
The reason why we have two zeros is because the degree of the polynomial is 2. If we find two numbers that adding we got -5 and multiplied 6 we solve the problem. For this case the solution is r =3, s =2

`y=(x -2)) (x-3)`

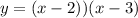
Explanation:

For this problem we have the following polynomial given:

`y = x^2 -5x +6`

And for this case we want to find the zeros or x interceps r and s so we want to rewrite the function on this way:

`y = (x-r) (x-s)`

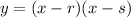
The reason why we have two zeros is because the degree of the polynomial is 2. If we find two numbers that adding we got -5 and multiplied 6 we solve the problem. For this case the solution is r =3, s =2

`y=(x -2)) (x-3)`