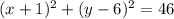Answer:
1) For
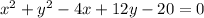 , the standard form is
, the standard form is
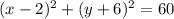
2) For
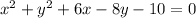 , the standard form is
, the standard form is
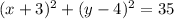
3) For
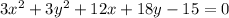 , the standard form is
, the standard form is
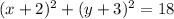
4) For
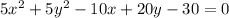 , the standard form is
, the standard form is
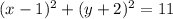
5) For
 , the standard form is
, the standard form is

6) For
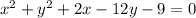 , the standard form is
, the standard form is
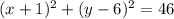
Explanation:
This can be done using the completing the square method.
The standard equation of a circle is given by
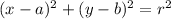
1) For
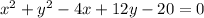
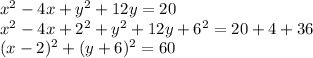
Therefore, for
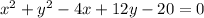 , the standard form is
, the standard form is
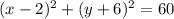
2) For
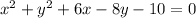
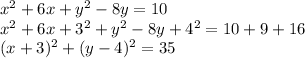
Therefore, for
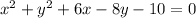 , the standard form is
, the standard form is
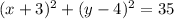
3) For
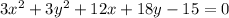
Divide through by 3
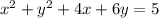
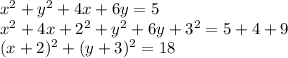
Therefore, for
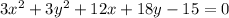 , the standard form is
, the standard form is
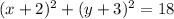
4) For
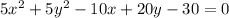
Divide through by 5
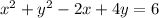
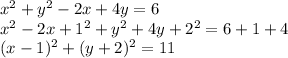
Therefore, for
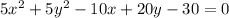 , the standard form is
, the standard form is
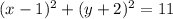
5) For

Divide through by 2
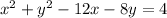
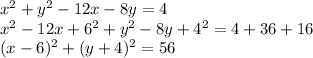
Therefore, for
 , the standard form is
, the standard form is

6) For
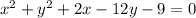
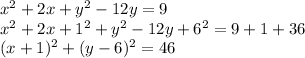
Therefore, for
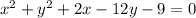 , the standard form is
, the standard form is