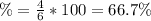Question

based off the data of ages of the last six US presidents( 69, 64, 46, 54, 47, and 70) What percentage of presidents ages fall within one standard deviation of the mean? (Round to one decimal place

Answer 1

`\bar X=(\sum_(i=1)^n X_i)/(n)`

`s=\sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)}`

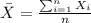
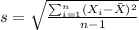
And replacing we got:

`\bar X= 58.33`

`s= 10.78`

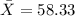
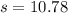
Then we can fin the limits for one deviation within the mean like this:

`\mu -\sigma = 58.33-10.78= 47.55`

`\mu -\sigma = 58.33+10.78= 69.11`

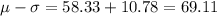
And then we see that the number of values between the limits are: 69, 64, 54,47 who represent 4 and then the percentage would be:

`\% =(4)/(6)*100 =66.7\%`

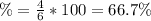
Explanation:

First we need ot calculate the mean and deviation with the following formulas:

`\bar X=(\sum_(i=1)^n X_i)/(n)`

`s=\sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)}`

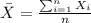
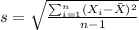
And replacing we got:

`\bar X= 58.33`

`s= 10.78`

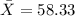
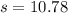
Then we can fin the limits for one deviation within the mean like this:

`\mu -\sigma = 58.33-10.78= 47.55`

`\mu -\sigma = 58.33+10.78= 69.11`

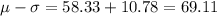
And then we see that the number of values between the limits are: 69, 64, 54,47 who represent 4 and then the percentage would be:

`\% =(4)/(6)*100 =66.7\%`