Question

Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x4 18x2 4 x5 30x3 20x dx

Answer 1

Your integrand is missing some symbols. My best interpretation is the following integral:

`I=\displaystyle\int(x^4+18x^2+4)/(x^5+30x^3+20x)\,\mathrm dx`

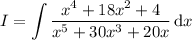
Decompose into partial fractions; we're looking for an expansion of the form

`(x^4+18x^2+4)/(x^5+30x^3+20x)=\frac ax+(bx^3+cx^2+dx+e)/(x^4+30x^2+20)`

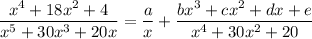
Now:

`x^4+18x^2+4=a(x^4+30x^2+20)+(bx^3+cx^2+dx+e)x`

`=(a+b)x^4+cx^3+(30a+d)x^2+ex+20a`

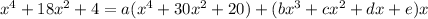
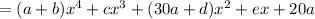
Matching up coefficients tells us that

`\begin{cases}a+b=1\\c=0\\30a+d=18\\e=0\\20a=4\end{cases}\implies a=\frac15,b=\frac45,d=12`

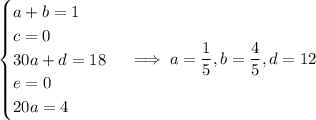
so that

`I=\displaystyle\frac15\int\frac{\mathrm dx}x+\frac45\int(x^3+15x)/(x^4+30x^2+20)\,\mathrm dx`

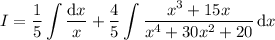
The integral is trivial:

`\displaystyle\frac15\int\frac{\mathrm dx}x=\frac15\ln|x|+C`

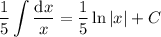
For the second integral, notice that

`\mathrm d(x^4+30x^2+20)=(4x^3+60x)\,\mathrm dx`

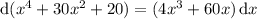
Distribute the 4 over the numerator, then substitute
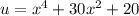`u=x^4+30x^2+20` and
`\mathrm du=(4x^3+60x)\,\mathrm dx`:

`\displaystyle\frac15\int(4x^3+60x)/(x^4+30x^2+20)\,\mathrm dx=\frac15\int\frac{\mathrm du}u=\frac15\ln|u|+C=\frac15\ln(x^4+30x^2+20)+C`

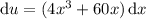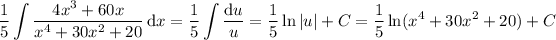
So we have

`I=\frac15\ln|x|+\frac15\ln(x^4+30x^2+20)+C`

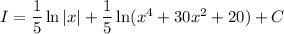
and with some simplification,

`I=\boxed{\ln\sqrt[5]x^5+30x^3+20x+C}`