Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s).

Consider the given function.

Answer 1

to determine the inverse of the given function, change f(x) to y, switch
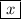`\boxed{x}` and y and solve for
`\boxed{y}`

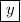
The resulting function can be written as

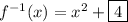`f^(-1)(x)=x^2+\boxed{4}` where
`x\geq\boxed{0}`

Explanation:

Hello,

f is defined for
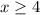`x\geq 4` as x-4 must be greater or equal to 0

and
`f(x)\geq 0`

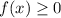
so
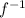`f^(-1)` is defined for
`x\geq 0`

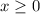
and then we can write

`x=(fof^(-1))(x)=f(f^(-1)(x))=\sqrt{f^(-1)(x)-4} \ so\\f^(-1)(x)-4=x^2 <=> f^(-1)(x)=x^2+4`

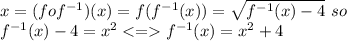
hope this helps