Question

Find the length of the side labeled x. Round intermediate values to the nearest tenth. Use the rounded values to calculate the next value. Round your final answer to the nearest tenth.

Answer 1

x = 42.2 units

Explanation:

By applying tangent rule in the right triangle ΔADC,

tan(44)° =
`\frac{\text{Opposite side}}{\text{Adjacent side}}`

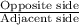
0.9657 =
`\frac{\text{AD}}{\text{DC}}`

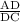
0.9657 =
`(AD)/(x)`

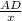
AD = 0.9657x

Now we apply cosine rule in ΔADB,

cos(30)° =
`\frac{\text{Adjacent side}}{\text{Hyptenuse}}`

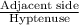
cos(30)° =
`\frac{\text{AD}}{\text{AB}}`

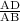
0.866 =
`(0.9657x)/(47)`

x =
`(47* 0.866)/(0.9657)`

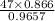
x = 42.15

x ≈ 42.2 units

Therefore, x = 42.2 units will be the answer.