Question

A sample of 1600 computer chips revealed that 43% of the chips do not fail in the first 1000 hours of their use. The company's promotional literature states that 41% of the chips do not fail in the first 1000 hours of their use. The quality control manager wants to test the claim that the actual percentage that do not fail is different from the stated percentage. Find the value of the test statistic. Round your answer to two decimal places.

Answer 1

Answer: The value of the test statistic is z= 1.63 .

Explanation:

Test statistic for proportion :

`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

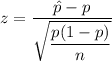
, where p =population proportion.

`\hat{p}` = sample proportion

n= sample size.

Let p be the proportion of chips do not fail in the first 1000 hours of their use.

As per given, we have

`p=0.41\\ n= 1600\\\hat{p}=0.43`

Then, required test statistic would be

`z=\frac{0.43-0.41}{\sqrt{(0.41(1-0.41))/(1600)}}\\\\=(0.02)/(√(0.0001511875))\\\\\approx(0.02)/(0.0123)\approx1.63`

Hence, the value of the test statistic is z= 1.63 .