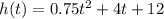Question

An evergreen nursery usually sells a certain shrub after 5 years of growth and shaping. The growth rate during those 5 years is approximated by dh/dt = 1.5t + 4, where t is the time in years and h is the height in centimeters. The seedlings are 12 centimeters tall when planted (t = 0). (a) Find the height after t years.

Answer 1

`h(t) = 0.75t^2 + 4t + 12`

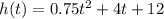
Explanation:

The equation given calculates the derivative of the height in relation to the time, that is, the rate of change of the height. To find the equation for the height, we need to integrate this equation:

`dh/dt = 1.5t + 4`

Multiplying both sides by 'dt', we have:

`dh = (1.5t + 4)dt`

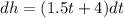
Using the integral in both sides:

`\int dh = \int (1.5t + 4) dt`

`h = 0.75t^2 + 4t + h(0)`

`h = 0.75t^2 + 4t + 12`

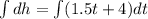
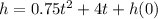
So the height after t years is represented by this equation:

`h(t) = 0.75t^2 + 4t + 12`