Answer:
(–1, –5)
Explanation:
Two linear equations are represented by using the tables below. A 2-column table with 4 rows titled Equation A. Column 1 is labeled x with entries negative 2, 0, 3, 4. Column 2 is labeled y with entries negative 8, negative 2, 7, 10. A 2-column table with 4 rows titled Equation B. Column 1 is labeled x with entries negative 3, negative 1, 1, 5. Column 2 is labeled y with entries negative 9, negative 5, negative 1, 7. The data points for equation A are graphed on the coordinate plane below and are connected by using a straight line. On a coordinate plane, a line goes through (0, negative 2) and (2, 4). What is the solution to the system of equations? (–2, –8) (–1, –5) (0, –2) (2, 4)
Answer: To find the equation of line A, we can use any two points. Let us use points (-2, -8) and (0, -2). Therefore, the equation of line A can be gotten using the equation:
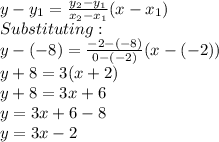
To find the equation of line B, we can use any two points. Let us use points (-3, -9) and (-1, -5). Therefore, the equation of line B can be gotten using the equation:

To find the solution to the system of equations, we solve them simultaneously
y = 3x - 2 . . . 1)
y = 2x - 3 . . . 2)
Subtracting equation 2 from 1:
x + 1 = 0
x = -1
Put x = -1 in equation 1)
y = 3(-1) - 2
y = -3 - 2
y = -5
Therefore the solution to the equation is (-1, -5)