Question

Use the given information to determine if the geometric series converges or

diverges. If it converges, find the sum.
ai = 0.75; r = 5
a) The series converges to 3.75.
b) The series converges to 0.15.
c) The series diverges. There is no sum.
d) The series converges to 20.

Answer 1

c) The series diverges. There is no sum.

Explanation:

A geometric series is a series of the form:

`S = \Sigma_(i=0)^(n) a\cdot r^(i)`,
`\forall i \in \mathbb{N}_(O)`

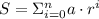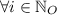
Where:

`a` - First term of the series, dimensionless.

`r` - Common ratio, dimensionless.

A geometric series converges only if
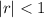`|r| < 1`. As
`r > 1`, the geometric series diverges. Hence, the right answer is C.