Question

What is the area of rhombus ABCD? Enter your answer in the box. Do not round at any steps.

Answer 1

Area of the rhombus ABCD = 16 square units

Explanation:

Area of a rhombus =
`(1)/(2)(\text{Diagonal 1})(\text{Diagonal 2})`

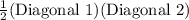
From the graph attached,

Diagonal 1 = Distance between the points A and C

Diagonal 2 = Distance between the points B and D

Length of a segment between (x₁, y₁) and (x₂, y₂) =
`\sqrt{(x_2-x_1)^(2)+(y_2-y_1)^2 }`

Diagonal 1 (AC) =
`√((4-0)^2+(-1+1)^2)` = 4 units

Diagonal 2(BD) =
`√((2-2)^2+(3+5)^2)` = 8 units

Now area of the rhombus ABCD =
`(1)/(2)(\text{AC})(\text{BD})`

=
`(1)/(2)* 4* 8`

= 16 units²

Therefore, area of the given rhombus is 16 units².