Question

PLEASE DONT REPORT VERY ERGANT FORGIVE MY GRAMMER and hand writing what kind of triangle is this please TY MUFFIN THE DOGGY

Answer 1

This is an acute, scalene triangle.

Explanation:

Alright, to find the type of triangle, let's use the distance formula (to find the length of the sides).

d =
`√((x_2-x_1)+(y_2-y_1))`

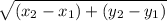
The distance from (2,3) to (5,0) is
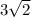`3√(2)`. = 4.24264068

The distance from (2,3) to (4,4) is
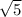`√(5)`. = 2.23606797

The distance from (5,0) to (4,4) is
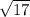`√(17)` . = 4.12310562

The length that is longest is
`3√(2)`.

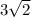Let's label it c.

Let's label the distance from (2,3) to (4,4) a.

Let's label the distance from (5,0) to (4,4) b.

If c^2 = a^2+b^2, this is a right triangle.

If c^2 < a^2+b^2, this is an acute triangle.

If c^2> a^2+b^2, this is an obtuse triangle.

(
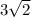`3√(2)`)^2 vs.(
`√(5)` )^2 +(
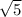`√(17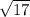)`)^2

18 vs. 5+ 17

18 vs 22.

c^2 < a^2 + b^2.

This is an acute triangle.

None of the sides are equal, so this is a scalene triangle.

This is an acute, scalene triangle.