Question

A top view of two walls of a room is represented by the x and y-axis, with units in meters. A ball is rolled from the point (0,15). It hits the adjacent wall at (20,0). Find the absolute value function that models the path of the ball. Determine when the ball passes within 3 meters of the wall represented by the x-axis.

Answer 1

The absolute value function that models the path of the ball is

`f(x) = \left | -(3)/(4)\cdot x + 15 \right |`

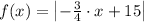
The coordinates when the ball passes within 3 meters of the wall is
`\left (3, 12\tfrac{3}{4} \right )`

Explanation:

Given that the ball rolls without other external influences, we have;

(y - 0) = (x - 15)

The slope, m is give by the relation;

m = (y₂ - y₁)/(x₂ - x₁)

m = (15 - 0)/(0-20) = -3/4

The equation of the path of the ball in slope and intercept form is presented as follows;

y = m·x + c

15 = -3/4 ×0 + c = 15

c = 15

The absolute value function that models the path of the ball is then;

`f(x) = \left | -(3)/(4)\cdot x + 15 \right |`

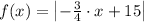
The vale of the function when x = 3 is given by the relation

`f(x) = \left | -(3)/(4)* 3 + 15 \right | = (51)/(4)`

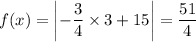
Therefore, we have the coordinates as
`\left (3, 12\tfrac{3}{4} \right )`.