Question

Find the lateral area of a regular square pyramid if the base edges are of length 12 and the perpendicular height is 8.

Answer 1

Answer: 240 units^2

Explanation:

LA= 1/2 Pl

P= perimeter of base

l= lateral height

l= 8^2 + (12/2)^2 = 10^2

P= 12 x 4 = 48

48 x 10 = 480

480/2 = 240

240 units^2

Answer 2

Lateral area of the pyramid = 120 square units

Explanation:

In the figure attached,

A pyramid has been given with square base with edges of 12 units and perpendicular height as 8 units.

Lateral area of a pyramid = Area of the lateral sides

Area of one lateral side =
`(1)/(2)(\text{Base})(\text{Lateral height})`

=
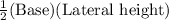
`(1)/(2)((b)/(2))(\sqrt{((b)/(2))^2+h^2})` [Since l =
`\sqrt{r^(2)+h^(2)}`]

=
`(1)/(2)(6)(√(6^2+8^2))`

=
`3√(100)`

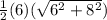
= 30 units²

Now lateral area of the pyramid = 4 × 30 = 120 square units