Question

A coordinate plane with 2 lines drawn. The first line is labeled f(x) and passes through the points (0, negative 2) and (1, 1). The second line is labeled g(x) and passes through the points (negative 4, 0) and (0, 2). The lines intersect at about (2.5, 3.2) How does the slope of g(x) compare to the slope of f(x)? The slope of g(x) is the opposite of the slope of f(x). The slope of g(x) is less than the slope of f(x). The slope of g(x) is greater than the slope of f(x). The slope of g(x) is equal to the slope of f(x). ALSO ITS NOT A NUMBER ANSWER

Answer 1

Option B.

Explanation:

If a line passing through two points, then the slope of line is

`m=(y_2-y_1)/(x_2-x_1)`

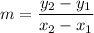
It is given that f(x) passing through the points (0,-2) and (1,1). So, slope of f(x) is

`m_1=(1-(-2))/(1-0)=1+2=3`

It is given that g(x) passing through the points (-4,0) and (0,2). So, slope of g(x) is

`m_2=(2-0)/(0-(-4))=(2)/(4)=(1)/(2)`

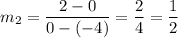
Since,
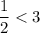`(1)/(2)<3`, therefore
`m_2<m_1`.

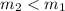The slope of g(x) is less than the slope of f(x).

Therefore, the correct option is B.