Question

An aging coyote cannot run fast enough to catch a roadrunner. He purchases on eBay a set of jet-powered roller skates, which provide a constant horizontal acceleration of 15.0 m/s2. The coyote starts at rest 70.0 m from the edge of a cliff at the instant the roadrunner zips past in the direction of the cliff.

Required:
a. Determine the minimum constant speed the roadrunner must have to reach the cliff before the coyote. At the edge of the cliff, the roadrunner escapes by making a sudden turn, while the coyote continues straight ahead. The coyote’s skates remain horizontal and continue to operate while he is in flight.
b. The cliff is 100 m above the flat floor of the desert. Determine how far from the base of the cliff the coyote lands.
c. Determine the components of the coyote’s impact velocity

Answer 1

a) v_correcaminos = 22.95 m / s , b) x = 512.4 m ,

c) v = (45.83 i ^ -109.56 j ^) m / s

Step-by-step explanation:

We can solve this exercise using the kinematics equations

a) Let's find the time or the coyote takes to reach the cliff, let's start by finding the speed on the cliff

v² = v₀² + 2 a x

they tell us that the coyote starts from rest v₀ = 0 and its acceleration is a=15 m / s²

v = √ (2 15 70)

v = 45.83 m / s

with this value calculate the time it takes to arrive

v = v₀ + a t

t = v / a

t = 45.83 / 15

t = 3.05 s

having the distance to the cliff and the time, we can find the constant speed of the roadrunner

v_ roadrunner = x / t

v_correcaminos = 70 / 3,05

v_correcaminos = 22.95 m / s

b) if the coyote leaves the cliff with the horizontal velocity v₀ₓ = 45.83 m / s, they ask how far it reaches.

Let's start by looking for the time to reach the cliff floor

y = y₀ +
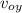`v_(oy)` t - ½ g t²

in this case y = 0 and the height of the cliff is y₀ = 100 m

0 = 100 + 45.83 t - ½ 9.8 t²

t² - 9,353 t - 20,408 = 0

we solve the quadratic equation

t = [9,353 ±√ (9,353² + 4 20,408)] / 2

t = [9,353 ± 13] / 2

t₁ = 11.18 s

t₂ = -1.8 s

Since time must be a positive quantity, the answer is t = 11.18 s

we calculate the horizontal distance traveled

x = v₀ₓ t

x = 45.83 11.18

x = 512.4 m

c) speed when it hits the ground

vₓ = v₀ₓ = 45.83 m / s

we look for vertical speed

v_{y} =
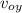`v_(oy)` - gt

v_{y} = 0 - 9.8 11.18

v_{y} = - 109.56 m / s

v = (45.83 i ^ -109.56 j ^) m / s