Question

ASK YOUR TEACHER Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? f(x) = x3 + x − 9, [0, 2]

Answer 1

Yes

Explanation:

The Mean Value Theorem states that if f(x) is defined and continuous on the interval [a,b] and differentiable on (a,b), then there is at least one number c in the interval (a,b) (that is a < c < b) such that

`f'(c)=(f(b)-f(a))/(b-a)`

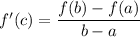
Given
`f(x)=x^3+x-9$ in [0,2]`

f(x) is defined, continuous and differentiable.

`f(2)=2^3+2-9=1\\f(0)=0^3+0-9=-9`

`f'(c)=(f(2)-f(0))/(2-0)=(1-(-9))/(2)=5`

`f'(x)=3x^2+1`

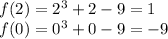
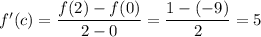
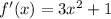
Therefore:

`f'(c)=3c^2+1=5\\3c^2=5-1\\3c^2=4\\c^2=(4)/(3) \\c=\sqrt{(4)/(3)} =1.15 \in [0,2]`

Since c is in the given interval, the function satisfy the hypotheses of the Mean Value Theorem on the given interval.