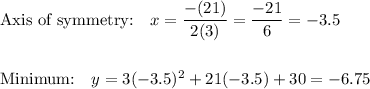Question

Jeremy and Arnold are working on a project for math class in which they are to identify the quadratic equation that represents a rain gauge that sits off the ground. Graph each of the equations and then determine which one could represent the position of the rain catcher that sits above the ground. The x-axis represents the ground. 1. y = x2 + 11x + 24 2. y = –x2 – 6x – 8 Direction of Parabola: ______ Direction of Parabola: ______ Location of vertex with respect Location of vertex with respect to the x axis: _____________ to the x axis: _____________ Determine if the graph depicts Determine if the graph depicts the rain gauge. ___________ the rain gauge. ___________ Why or why not? ___________ Why or why not? ___________ _________________________ _________________________ _________________________ _________________________ 3. y = x2 – 2x + 3 4. y = x2 + 4x + 4 Direction of Parabola: ______ Direction of Parabola: ______ Location of vertex with respect Location of vertex with respect to the x axis: _____________ to the x axis: _____________ Determine if the graph depicts Determine if the graph depicts the rain gauge. ___________ the rain gauge. ___________ Why or why not? ___________ Why or why not? ___________ _________________________ _________________________ _________________________ _________________________ 5. y = 3x2 + 21x + 30 Direction of Parabola: ______ Location of vertex with respect to the x axis: _____________ Determine if the graph depicts the rain gauge. ___________ Why or why not? ___________ _________________________ _________________________

Answer 1

Answer: see below

Explanation:

Given ax² + bx + c = 0

If a > 0 (positive), then parabola opens UP

If a < 0 (negative), then parabola opens (DOWN)

Axis of Symmetry:
`x=(-b)/(2a)`

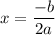
Max/Min: Plug axis of symmetry into the given equation and solve for y.

1) y = x² + 11x + 24

a=1 b=11

a> 0 so parabola opens UP

`\text{Axis of symmetry:}\quad x=(-(11))/(2(1))=(-11)/(2)=-3.5\\\\\\\text{Minimum:}\quad y=(-3.5)^2+11(-3.5)+24 = -6.25`

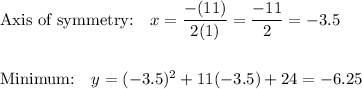
2) y = -x² - 6x - 8

a=-1 b=-6

a< 0 so parabola opens DOWN

`\text{Axis of symmetry:}\quad x=(-(-6))/(2(-1))=(6)/(-2)=-3\\\\\\\text{Maximum:}\quad y=(-3)^2-6(-3)-8 = 1`

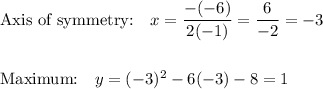
3) y = x² - 2x + 3

a=1 b=-2

a> 0 so parabola opens UP

`\text{Axis of symmetry:}\quad x=(-(-2))/(2(1))=(2)/(2)=1\\\\\\\text{Minimum:}\quad y=(1)^2-2(1)+3 = 2`

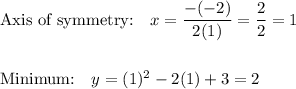
4) y = x² + 4x + 4

a=1 b=4

a> 0 so parabola opens UP

`\text{Axis of symmetry:}\quad x=(-(4))/(2(1))=(-4)/(2)=-2\\\\\\\text{Minimum:}\quad y=(-2)^2+4(-2)+4 = 0`

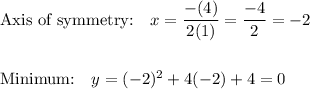
5) y = 3x² + 21x + 30

a=3 b=21

a> 0 so parabola opens UP

`\text{Axis of symmetry:}\quad x=(-(21))/(2(3))=(-21)/(6)=-3.5\\\\\\\text{Minimum:}\quad y=3(-3.5)^2+21(-3.5)+30 = -6.75`