Question

Suppose a population grows according to a logistic model with initial population 500 and carrying capacity 5,000. If the population grows to 1250 after one year, what will the population be after another three years

Answer 1

4,500

Step-by-step explanation:

The logistic growth model is given by:

`(dP)/(dt)=rP(1-(P)/(K) )`

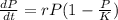
Solving for P(t), we obtain:

`P(t)=(KP_0e^(rt))/((K-P_0)+P_0e^(rt))$ where:\\P_0=$Initial Population\\K=Carrying Capacity\\r=Growth rate\\P(t)=Population at a time t.`

We are given that:

`I$nitial Population,P_0=500\\$Carrying Capacity,K=5000\\Population after one year, P(1)=1250 \implies t=1`

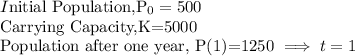
Therefore:

`1250=(500 * 5000e^(r * 1))/((5000-500)+500e^(r* 1))\\\\1250[(5000-500)+500e^(r)]=500 * 5000e^(r)\\4500+500e^(r)=2000e^(r)\\2000e^(r)-500e^(r)=4500\\1500e^(r)=4500\\e^r=3\\$Take the natural logarithm of both sides\\r =\ln 3`

We want to determine the population after another three years. i,e When t=4

`P(4)=(500 * 5000e^(\ln|3| * 4))/((5000-500)+500e^(\ln|3| * 4))\\=(2,500,000e^(\ln|3| * 4))/(4500+500e^(\ln|3| * 4))\\P(4)=4500`

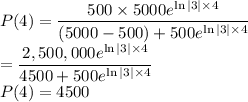
Therefore, after another three years, the population will be 4500.