Question

The frequency of a physical pendulum comprising a nonuniform rod of mass 1.15 kg pivoted at one end is observed to be 0.658 Hz. The center of mass of the rod is 42.5 cm below the pivot point. What is the rotational inertia of the pendulum around its pivot point

Answer 1

The rotational inertia of the pendulum around its pivot point is
`0.280\,kg\cdot m^(2)`.

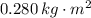Step-by-step explanation:

The angular frequency of a physical pendulum is measured by the following expression:

`\omega = \sqrt{(m\cdot g \cdot d)/(I_(o)) }`

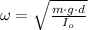
Where:

`\omega` - Angular frequency, measured in radians per second.

`m` - Mass of the physical pendulum, measured in kilograms.

`g` - Gravitational constant, measured in meters per square second.

`d` - Straight line distance between the center of mass and the pivot point of the pendulum, measured in meters.

`I_(O)` - Moment of inertia with respect to pivot point, measured in
`kg\cdot m^(2)`.

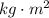In addition, frequency and angular frequency are both related by the following formula:

`\omega =2\pi\cdot f`

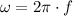
Where:

`f` - Frequency, measured in hertz.

If
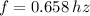`f = 0.658\,hz`, then angular frequency of the physical pendulum is:

`\omega = 2\pi \cdot (0.658\,hz)`

`\omega = 4.134\,(rad)/(s)`

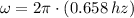
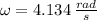
From the formula for the physical pendulum's angular frequency, the moment of inertia is therefore cleared:

`\omega^(2) = (m\cdot g \cdot d)/(I_(o))`

`I_(o) = (m\cdot g \cdot d)/(\omega^(2))`

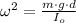
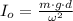
Given that
`m = 1.15\,kg`,
`g = 9.807\,(m)/(s^(2))`,
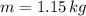`d = 0.425\,m` and
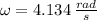`\omega = 4.134\,(rad)/(s)`, the moment of inertia associated with the physical pendulum is:

`I_(o) = ((1.15\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (0.425\,m))/(\left(4.134\,(rad)/(s) \right)^(2))`

`I_(o) = 0.280\,kg\cdot m^(2)`

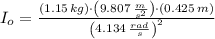
The rotational inertia of the pendulum around its pivot point is
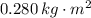`0.280\,kg\cdot m^(2)`.