Question

Un proyectil es lanzado horizontalmente desde una altura de 12 metro con una velocidad de 80 m/sg. a.Calcular el tiempo de vuelo b. Su alcance horizontal y velocidad de impacto contra el suelo.

Answer 1

t= 1,56 s , x= 124,8 m , v = (80 i^ - 15,288 j ) m/s

Step-by-step explanation:

Este es un ejercicio de lanzamiento proyectiles, comencemos por encontrar el tiempo que tarda en llegar al piso

y = y₀ +
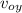`v_(oy)` t – ½ g t²

en este caso la altura inicial es y₀= 12 m y llega a y=0 , como es lanzado horizontalmente la velocidad vertical es cero (v_{oy}=0)

0 = y₀ – ½ g t²

t= √ (2 y₀/g)

calculemos

t= √ ( 2 12 / 9,8)

t= 1,56 s

El alcance del proyectil es la distancia horizontal recorrida

x = v₀ₓ t

x = 80 1,56

x= 124,8 m

La velocidad de impacto cuando toca el suelo

vx = v₀ₓ = 80 ms

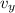`v_(y)` = v_{oy} – gt

v_{y} = - 9,8 1,56

v_{y} = - 15,288 m/s

la velocidad es

v = (80 i^ - 15,288 j ) m/s

Traducttion

This is a projectile launching exercise, let's start by finding the time it takes to reach the ground

y = y₀ + v_{oy} t - ½ g t²

in this case the initial height is i = 12 m and it reaches y = 0, as it is thrown horizontally the vertical speed is zero (
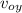`v_(oy)` = 0)

0 =y₀I - ½ g t²

t = √ (2y₀ / g)

let's calculate

t = √ (2 12 / 9.8)

t = 1.56 s

Projectile range is the horizontal distance traveled

x = v₀ₓ t

x = 80 1.56

x = 124.8 m

Impact speed when it hits the ground

vₓ = v₀ₓ = 80 ms

v_{y} = v_{oy} - gt

v_{y} = - 9.8 1.56

v_{y} = - 15,288 m / s

the speed is

v = (80 i ^ - 15,288 j) m / s