A circle has a central angle measuring StartFraction 7 pi Over 10 EndFraction radians that intersects an arc of length 33 cm. What is the length of the radius of the circle? Rou…

Question

asked Sep 24, 2021 98.6k views

2 Answers

Ipor Sircer · Answer 1 · 2021-09-29T03:18:44+0000

Answer:

15 cm.

Explanation:

It is given that,

Central angle
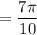
$=(7\pi)/(10)$

Arc length = 33 cm

Formula for arc length :

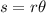
$s=r\theta$

where, s is arc length, r is radius and
$\theta$ is central angle in radian.

Substitute s=33 and
$\theta=(7\pi)/(10)$ in the above formula.

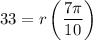
$33=r\left((7\pi)/(10)\right)$

Multiply both sides by 10.

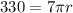
$330=7\pi r$

Divide both sides by
$7\pi$ .

$(330)/(7\pi)= r$

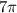Put
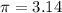
$\pi=3.14$

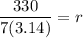
(330)/(7(3.14))= r

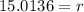
15.0136= r

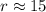
$r\approx 15$

Therefore, the radius of the circle is 15 cm.