Answer:

And for this case the confidence interval is given by:
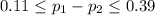
Since the confidenc einterval not contains the value 0 we can conclude that we have significant difference between the two population proportion of interest 1% of significance given. So then we can't conclude that the two proportions are equal
Explanation:
Let p1 and p2 the population proportions of interest and let
 and
and
 the estimators for the proportions we know that the confidence interval for the difference of proportions is given by this formula:
the estimators for the proportions we know that the confidence interval for the difference of proportions is given by this formula:

And for this case the confidence interval is given by:
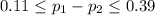
Since the confidence interval not contains the value 0 we can conclude that we have significant difference between the two population proportion of interest 1% of significance given. So then we can't conclude that the two proportions are equal