Question

A random sample of 85 group leaders, supervisors, and similar personnel revealed that a person spent an average 6.5 years on the job before being promoted. The population standard deviation was 1.7 years. Using the 0.95 degree of confidence, what is the confidence interval for the population mean?

Answer 1

95% of confidence interval for the Population

( 6.1386 , 6.8614)

Explanation:

Step( i ):-

Given random sample size 'n' =85

Mean of the sample size x⁻ = 6.5 years

Standard deviation of Population = 1.7 years

Level of significance = 0.95 or 0.05

Step(ii):-

95% of confidence interval for the Population is determined by

`(x^(-) - Z_(0.05) (S.D)/(√(n) ) , x^(-) + Z_(0.05) (S.D)/(√(n) ))`

`(6.5 - 1.96(1.7)/(√(85) ) , 6.5 + 1.96 (1.7)/(√(85) ))`

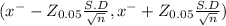
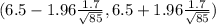
( 6.5 - 0.3614 , 6.5 + 0.3614 )

( 6.1386 , 6.8614)

Conclusion:-

95% of confidence interval for the Population

( 6.1386 , 6.8614)